通常都是由人眼来主观判断图像的质量高低,能否通过数学度量对判定图像的质量呢?比如通过图片的像素/亮度/边缘数量来判断图像是清晰还是模糊。
前言
通常都是由人眼来主观判断图像的质量高低,能否通过数学度量对判定图像的质量呢?比如通过图片的像素/亮度/边缘数量来判断图像是清晰还是模糊。
看似简单,但实际上很困难,图像是信息的载体,载体的质量高,并不意味着信息内容的质量高,比如拍摄者是为了突出物体虚化的背景,或者拍摄者是为了拍摄风景,虚化的人物。从数据上很难客观的评判图片中的内容是否高质量。
我们可以通过数学模型,给出原图与待评图之间的差异量,再辅以人眼筛选,综合判断图片的质量。
图像质量评估体系(IGA)
图像质量评估算法是对任意的图像进行质量评分,将图像整体作为输入,将图像的质量得分作为输出,图像质量评估分为三种:
- 全原图质量评估:在这种方法中,我们拥有一个非失真的图像,以测量待评图像的质量。在我们可以拥有原始图像及其压缩图像的情况下,此方法可用于待评图像压缩算法的质量。
- 降低参考的图像质量评估:在这种方法中没有可以用来参考的图像,但是具有参考信息的图像(例如,带有水印的图像)可以比较和测量待评图像的质量。
- 无原图质量评估:算法获得的唯一输入是要测量其质量的图像,完全没有可以用来参考的图像,因此被称为无参考“No-Reference”
草案
本方案的目的是判断原图片通过裁剪/渲染后的图片质量变化的程度。
环境变量上,我们可以获得原图和待评图,并且样图是可以固定的,所以可以使用全参考模式来制定方案。
我们需要找几种常见类型的样图,如人像,风景照等
使用不同的方式去编辑渲染,再计算评分。
比如:
- 使用【方式1】渲染的图A,与原图比较差异。计算获得评分X
- 使用【方式2】渲染的图B,与原图比较差异。计算获得评分Y
比较 X 与 Y 的评分,再辅以人眼筛选,确定差异值。我们将首次评分的结果作为基准值。
后续每次渲染方式的变更时,都将进行样图的重评。
如此我们便可知道当前渲染的图片质量是提升了还是在裂化。
主流评估方案
基于图像像素统计
计算待评图和原图对应像素点值的差异,从统计角度衡量图像质量优劣。
待评图为F,原图为R,大小都为M*N。
均方差 MSE(Mean Squared Error)
是反映原图与待评图之间差异程度的一种度量。思路是对两张尺寸完全相同的图片一个个像素进行对比,对比的数值就是图像的色值。
该方案不考虑人眼的局部视觉因素,因此无法用于判断图像的局部质量。
参考结论: 取值范围为[0,+∞),当预测值与真实值完全吻合时等于0,即完美模型;该值越大,差异越大。该值越小,差异性越小,图片质量越高
计算公式:
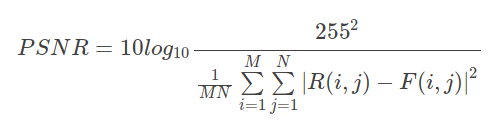
def mse(origin, target):
# the 'Mean Squared Error' between
# the two images is the sum of the squared difference between the two images
mse_error = np.sum((origin.astype("float") - target.astype("float"))**2)
mse_error /= float(origin.shape[0] * origin.shape[1])
# return the MSE. The lower the error, the more "similar" the two images are.
return mse_error
即峰值信噪比 PSNR(Peak Signal to Noise Ratio)
最为广泛使用的一种图像评价,通常用来比较待评图与原图的质量差异。
其原理是比较最大值信号与背景噪音之间的差异。
PSNR也具有局限性,人眼的视觉对误差的敏感度不是绝对的,其产值结果可能会受到亮度或对比度的影响。可能出现PSNR值较高的图像,但是肉眼判断为不清晰的情况。
OpenCV官方文档说这也是逐帧比较视频差异的最常用方式,毕竟它简单,运行速度快。但其呈现的差异有时候与人的主观感受不一致,所以OpenCV还提供了结构相似性算法SSIM做出改进。
参考结论:取值范围为(0,∞),值越高,表示是待评图与原图的差异越小,即质量越高
计算公式:也是在MSE基础上的进一步扩展,这里MAX表示图像颜色最大值,8bit图像取值为255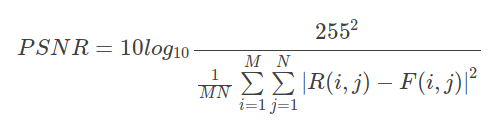
def PSNR(original, target):
mse = np.mean((original - target)**2)
if (mse == 0):
return 100
max_pixel = 255.0
psnr = 20 * log10(max_pixel / sqrt(mse))
return psnr
基于结构信息基础
提出者认为图像的结构失真的度量应是图像感知质量的最好近似。在此基础上提出了结构相似性度量。
结构相似度 SSIM(Structural Similarity Index)
结构相似性,是一种衡量两幅图像相似度的指标。该指标首先由德州大学奥斯丁分校的图像和视频工程实验室(Laboratory for Image and Video Engineering)提出。
自然图像具备高度结构性,临近的像素间存在强相关性,而这样的关系性承载了场景中物体的结构信息。人类视觉系统在观看图像时已经很习惯抽取这样的结构性信息。因此,在设计图像质量衡量指标用以衡量图像有损程度时,结构性有损的衡量是很重要的一环。
SSIM考虑了人眼的生物特征,是基于感知的计算模型,人类视觉系统就是从可视区域内获取结构信息,所以我们也可以检测结构信息的差异来对比图片,这和MSE或者PSNR通过线性变换来分解信号有本质上的不同。
参考结论:取值范围为(0, 1],数值越大,表示差异性越小,1代表两幅图像完全相同。
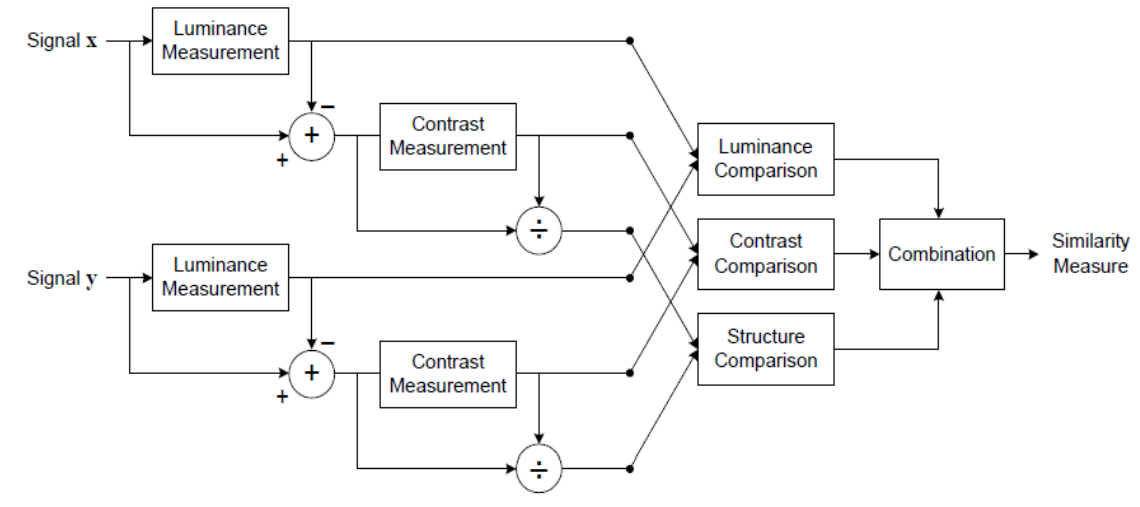
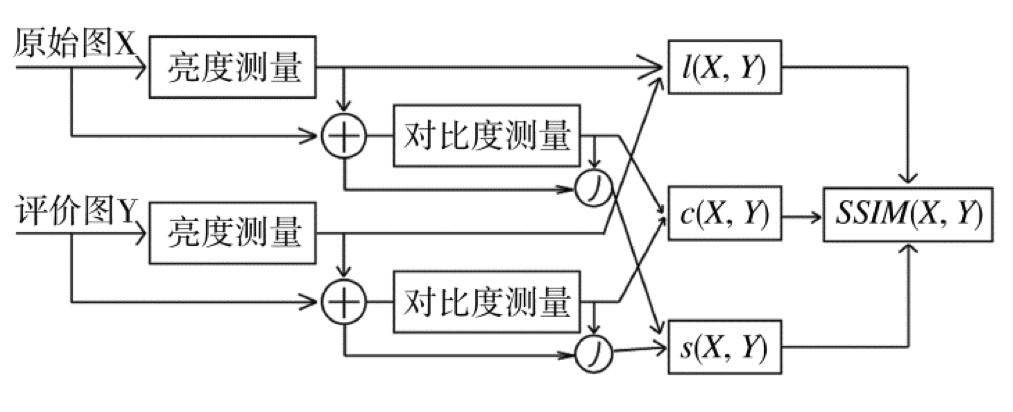
计算公式:SSIM的测量体系由三个模块组成: 亮度,对比度和结构。其中 l(x, y)是亮度比较,c(x, y)是对比度比较,s(x, y)是结构比较。
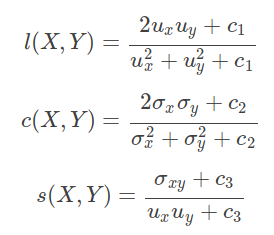
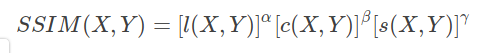
from skimage.metrics import structural_similarity as ssim
ssim(origin, target)
基于信息论基础
基于信息论中的信息熵基础
视觉信息保真度 VIF(Visual Information Fidelity)
VIF是Sheikh等结合自然图像统计模型、图像失真模型和人眼视觉系统模型提出的图像质量评价指标. 与峰值信噪比(Peak Signal-to-Noise Ratio, PSNR)、结构相似性(Structural Similarity, SSIM)等指标相比,VIF与主观视觉有更高的一致性。其值越大,表明图像质量越好。
信息保真度准则 IFC(Information Fidelity Criterion)
通过计算待评图像和原图之间的互信息来衡量图像的质量优劣。扩展了图像与人眼之间的联系。
缺点:对图像的结构信息没有反应。
演示案例

从样图可以得出结论,当MSE值小,PSNR大,SSIM值接近 1 时,图片的质量是最高的。
定量评分方案
技术指标
选用MSE、PSNR、SSIM综合分析原图与导出图的质量差异。
全图导出
比较原图与App导出后的图片以得出全图导出功能的评分。
样图原图尺寸: 3264 × 2448
| AAA | BBB | CCC | |
|---|---|---|---|
| File Size | 1.9 MB | 3.2 MB | 2.4 MB |
| Pixel | 3240 × 2430 | 3264 × 2448 | 3264 × 2448 |
| MSE | 24.580809200833205 | 22.164186650967576 | 2.5357344530949635 |
| PSNR | 42.30787129372325 | 49.05336805988961 | 44.094927024491255 |
| SSIM | 0.9837596127093489 | 0.9970888021806221 | 0.9892957811791622 |
数据上差异并不是很明显,AAA对像素进行了一定的裁剪,产出图片的体积更小,质量较高。
MSE的差异来自于CCC右下角没有水印,AAA 与 BBB都有水印
图片编辑
编辑功能会对原图内容进行修改,无法直接和原图进行比较,我们需要先对现有功能的导出图进行采样,确定基准值。
- 通过质量最大化的渲染方案A,获得一张肉眼判断为高质量的编辑后图片,作为原图。
- 选用兼顾性能与质量的渲染方案B,通过相同的编辑参数处理图片,作为待评图。
- 应用MSE、PSNR、SSIM对两张图进行差异化分析,获得评分X。
- 评分X即可作为基准值,后续有新的方案,则重复1-3的步骤,获得新的评分。与基准值X做比较,来判断新方案的优化幅度。
